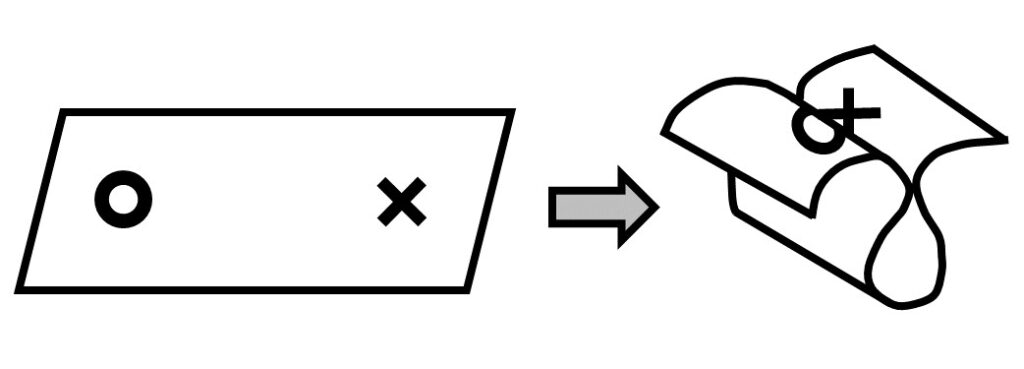
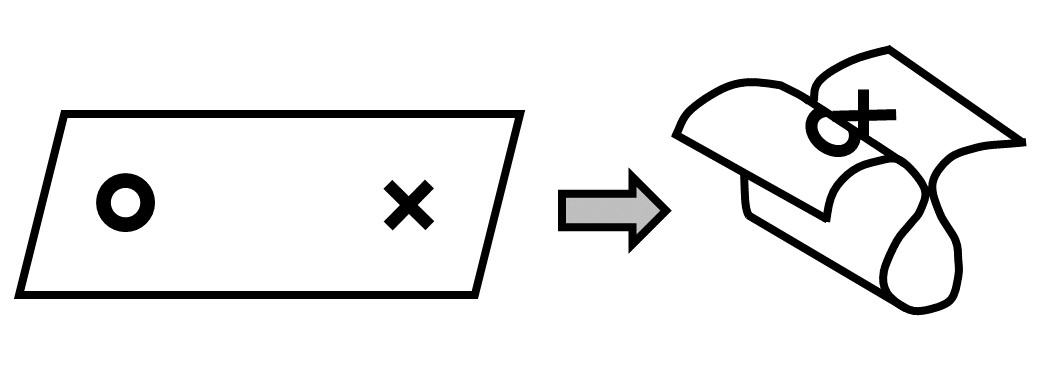
宇宙が舞台のSF作品ではワープがよく登場し、長距離移動のために空間を歪ませて近道する原理を紙を折り曲げる事で説明する描写が良く見られます（上図）。日本では「ドラえもん のび太の宇宙開拓史(1980)」が有名ですが海外映画でも見られます。最古は何なのか？どういう系譜を辿ってきたのか？色々情報を集めました。
まずは全容
まずは調査範囲での全容を図解します。このブログはドラえもんメインですので、藤子・F・不二雄が描いた紙曲げが何から来ているのか、海外での使用例と関係あるのかという観点で調査してますので、後期のフォロワー例は追いきれておらず、もっとたくさんあると思います。
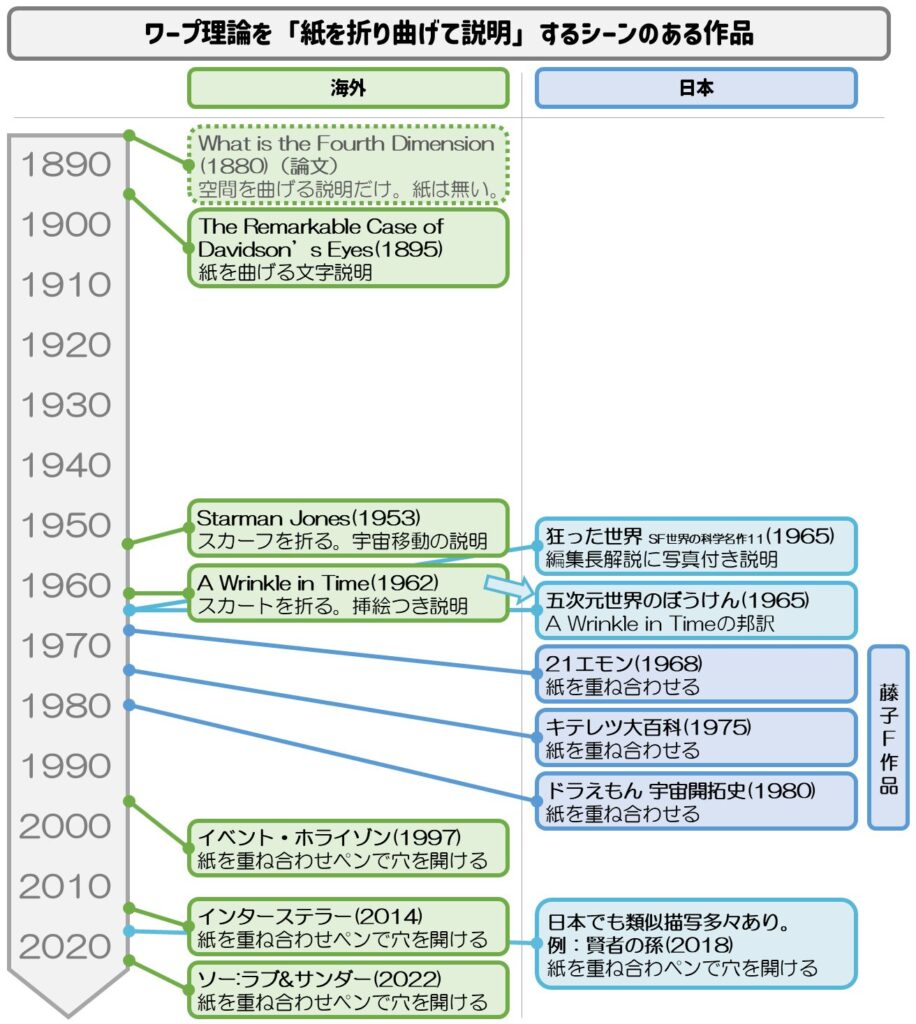
推測では「古い海外に始祖があり、それを日本ではF先生が広め、海外も始祖から広がった」って感じなのかなと思っています。詳細と総括は後半に書きます。
F先生の作品で登場する例
漫画：21エモン「超特急ロケット」(1968 藤子・F・不二雄)
私が知る限り紙を曲げる系のワープ説明の最初の日本作品です。1968年8号の週刊少年サンデー掲載の21エモン「超特急ロケット」の回。ロケットがワープ状態に入った際に、主人公21エモンがワープを知らなかったので専属メイドが説明する形で出てきます。
メイド「たとえばこの◎から✕へいちばんやはくいくには、どうしたらいいでしょう。」
21エモン「ふたつをむすんだ直線が、いちばん近道だ。」
メイド「いいえ。こうすればいいんです。」
21エモン「あインチキ！！」
メイド「これがワープ航法なんです。空間をゆがめてすっとばしちゃうんですのよ。」
21エモン「へええ そんなことができるの。」引用元：藤子・F・不二雄「21エモン」「超特急ロケット」
上記のセリフの形で、21エモンが直線を引くが、メイドは紙を折り曲げて最短距離を説明します。1981年映画化した際にも登場しました。F先生はこの後も計３作品で同じ説明描写を入れていきます。
漫画：キテレツ大百科「らくらくハイキング」(1975 藤子・F・不二雄)
1975年11月号「こどもの光」に掲載のキテレツ大百科「らくらくハイキング」の回。主人公キテレツがハイキングに重い荷物を持って行きたくないので「天狗のぬけあな」という２個所の離れた空間をくっつける発明品を作り、下記の説明がされます。
キテレツ「近道をつくるそうちだよ。そうだな、わかりやすくせつ明すると…。テープの上に二つの点をかく。
この点から点へ行く、いちばんの近道はどこだろう。」
コロ助「そんなのわかりきったことナリ。点と点をむすぶ直線、これ以上の近道はないナリ！」
キテレツ「そこがおまえの考えのあさいとこなんだ。テープを曲げて、点をくっつければいい。」
コロ助「ずるい、インチキナリ。」引用元：藤子・F・不二雄「キテレツ大百科」「らくらくハイキング」
細長いテープを使って説明し、テープを曲げて●と●を重ね合わせます。
他の例では宇宙移動のような長大なワープで使われるのですが、キテレツは自宅から山への移動と言うずいぶん庶民的な使い方をします。
漫画：「ドラえもん のび太の宇宙開拓史」(1980 藤子・F・不二雄)
1980年9月号のコロコロ「ドラえもん のび太の宇宙開拓史」で登場します。ゲストキャラの宇宙人ロップルがのび太にワープの仕組みを教えるため下記の説明をします。
ロップル「この紙を宇宙としよう。」
のび太「うんうん。」
ロップル「AからBの星へ、なるべく早く行くには、どうすればいい？」
のび太「どうすればって……一直線にこう……。」
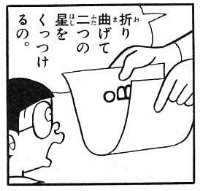
ロップル「いや、もっと早く行けるよ。折り曲げて二つの星をくっつけるの。これが、つまりワープなのさ。」引用元：藤子・F・不二雄「ドラえもん のび太の宇宙開拓史」
紙に○Aと○Bを書き最短経路を問います。のび太はその間を直線でつなぎますが、ロップルは紙を折り曲げてABをくっつけこれが最短だと説明します。
日本で最も有名な紙ワープ説明ではないでしょうか。ちなみにこの説明は原作漫画にありますが大山のぶ代時代の映画版(1981)ではこの説明は省略されており登場しません。水田わさび版「新・のび太の宇宙開拓史(2009)」ではこの説明がちゃんと登場します。
ドラえもん以降で見られる事例
映画「イベント・ホライゾン」（1997 アメリカ）
1997年8月15日公開の「イベント・ホライゾン」は宇宙を舞台にしたSF作品で、ワープが可能な宇宙船イベント・ホライゾン号のワープ装置の説明として、装置開発者の主人公ウェアー博士が宇宙船クルー達に説明するために紙の説明が入ります。チラシの紙の２個所にペンで穴を開け、その紙を折りたたんで穴同士をくっつけて、さらにそこにペンで貫通させる事でワームホールの説明をします。
映画「インターステラー」(2014 アメリカ)
2014年11月7日公開の「インターステラー」では、誰かによって作られたワームホールに飛び込み遠い宇宙に移動する物語が展開しますが、物理学者ロミリー博士が主人公クーパーにワームホールの説明をする形で登場します。
ロミリー「ここから移動をする。ここに。だが遠い。ワームホールがこんな風に２点をつなげる。時空の超越だ。」
引用元：映画「インターステラー」(2014)
上記のセリフと共に、メモ用紙の２箇所に✕を書き、そこを直線で繋ぐが「だが遠い」と説明、そして紙を折り曲げ２点を重ね合わせ、「こんな風に」とペンで✕の箇所に穴を開けてこれがワームホールであると説明します。自分達の力で空間を歪ませるというワープではなく、誰かがすでに歪ませておいてくれた事で存在するワームホールの説明として使われます。
漫画版「賢者の孫」(2018 日本)
2018年7月 Web漫画雑誌「ヤングエースUP」連載の「賢者の孫(漫画版)」では主人公シンが空間移動ゲートのイメージを仲間に下記のように説明します。
シン「この地点Aから地点Bまでの最短距離ってどう行けばいい？」
引用元：漫画：緒方俊輔「賢者の孫」
「そんなの簡単だよ！AからBまで一直線に行けばいいんでしょ？」
シン「ブー そのイメージじゃ直接歩いて移動するのと変わらない」
（中略）
シン「まずAとBがちょうど重なり合うように紙を折る これでAとBが内部で接した状態になるな この紙を空間 Aを自分のいる場所 Bを行きたい場所とすると 紙を折り曲げた時点で距離がゼロになる つまり これが最短距離であり…… この『穴』がゲートだ」
紙を折り曲げ○Aと○Bを重ね合わせ、ペンで穴を開けて最短距離の説明をします。なおこのシーン、ネット界隈では「ドラえもんのパクリ」という文脈でイジられる事が多いようです。確かに0から思いついたアイデアではなく何か参考にした可能性は高いでしょうが、ドラえもんを直接的に参照したかは不明です。むしろペンで穴を開ける演出は藤子作品には無く海外映画でよく見られるので参考にしたのはそっちの可能性が高いと思います。
映画「ソー:ラブ&サンダー」(2022 アメリカ) 他映画の使用例に触れながら
2022年7月8日公開「ソー:ラブ&サンダー」では天体物理学者ジェーンがワームホールの説明をする際に本の２個所にA,Bマークを付け、最短経路を実現する方法として紙を折り曲げペンで穴を空けます。その際ジェーンは説明相手に「イベント・ホライゾンって映画見た？インターステラーは？」と質問をして、見たこと無いと回答したため説明を始めるという流れです。過去映画をストレートにセリフに登場させて、「ご存知の有名な説明ですが知らない人のために」という感じで説明に入ります。
なおこの映画のワープは主人公ソーの神の力によるもので、科学的に説明する必要性はそんなにないです。
始祖とF先生の接点は何か？
このように世界中で使用例があるのですが、F先生の作品を海外勢がマネしたとはさすがに思えない。もっと古い共通の始祖があるのでは…と思っていたら100年以上前の作品がありました。
小説「デイヴィドソンの不思議な目(1895 イギリス)」(H・G・ウェルズ)
調べた限り最古の例はなんと1895年でSFの巨匠H.G.ウェルズの作品です。短編「The Remarkable Case of Davidson’s Eyes（ダヴィドソンの眼の異様な体験）」は、なぜか視界が遠く離れた場所と繋がってしまった男の奇妙な体験の話です。空間がねじれてくっついた理由の説明を下記のようにします。宇宙ワープではないですが遠方をひとっ飛びにつなげる説明です。
his explanation invokes the Fourth Dimension, and a dissertation on theoretical kinds of space. To talk of there being “a kink in space” seems mere nonsense to me; it may be because I am no mathematician. When I said that nothing would alter the fact that the place is eight thousand miles away, he answered that two points might be a yard away on a sheet of paper, and yet be brought together by bending the paper round.
引用元：H・G・ウェルズ「The Remarkable Case of Davidson’s Eyes (1895)」
（ざっくり翻訳）
「空間のねじれが存在するなんてナンセンスだ、8000マイル離れている事実は変わらないという指摘に対し、ウェイド教授は四次元と理論的な空間に関する論文を引き合いに出し、「紙の上では2点が1ヤード離れたところにあっても紙を丸く曲げることによって1つに集まるかもしれない。」と答えた。
H.G.ウェルズは超有名なSF作家。海外クリエイターも読む機会は十分あります。F先生も当然ウェルズを知っています1。これを読んでいたとすれば事は簡単ですが、邦訳本が当時あったのか国会図書館のHPで調べても一番古いのが「ザ・ベスト・オブ・H・G・ウエルズ(サンリオSF文庫)(1981年6月)」しか引っかからず、21エモンの1968年以前にF先生が読んだ可能性は特定できませんでした。
本当に論文はある？
作中では論文からの引き合いという形で紙曲げ理論を説明します。
実際に論文があり引用したのか、それとも架空の論文を演出として登場させたのか。調べるとその辺りを調べているTwitterがありまして、1880年チャールズ・ハワード・ヒントンの論文「What is the Fourth Dimension(四次元とは何か)」がルーツの可能性があるようです。紙ではなく「平面を曲げる」という抽象的な説明になっているので、理論としてここで登場し、それを分かりやすい説明にするために紙を曲げる比喩に変化させたのがウェルズという感じなのかもしれません。
小説「スターマン・ジョーンズ」(1953 アメリカ)宇宙間移動に使った事例。
長大な宇宙間移動としてのワープ説明に使った初期例はSFの巨匠ロバート・A・ハインラインの小説「スターマン・ジョーンズ」があります。宇宙に憧れる男マックスが様々な偶然に巻き込まれて宇宙旅行に行く話で、下記ワープの説明が登場します。
Could you lend me that scarf you’re wearing for a minute?”
引用元：Robert A. Heinlein “Starman Jones”(1953)
“Huh? Why, sure.” She removed it from her neck.
It was a photoprint showing a stylized picture of the solar system, a souvenir of Solar Union Day.
(中略)
“Hush a moment. Here’s Jupiter. To go from Mars to Jupiter you have to go from here to here, don’t you?“
“Obviously.”
“But suppose I fold it so that Mars is on top of Jupiter? What’s to prevent just stepping across?“
（要約してざっくり翻訳）
（主人公マックスは太陽系の絵が描かれたスカーフを借りて説明する。）
「ここに描かれた火星から木星に行くには、ここからここまで移動しなきゃならないだろ？でも、もしこうやって折り曲げて、火星を木星の上に重ねたら？一歩で行けるじゃないか？」
ハインラインも超一流SF作家。F先生も当然知っており代表作「夏への扉」はドラえもんの着想元の一つという説もあるくらいです2。しかしスターマン・ジョーンズを読んでいたかというと英語原作こそ1953年ですが日本語訳版が出たのは1979年なので、21エモンの1968年より後です。当時の状況的にF先生が読んでいた可能性は特定できません。
小説「A Wrinkle in Time (1962 アメリカ)」(邦題「五次元世界のぼうけん」)図が登場した初期作品。
マデレイン・レングルの小説「A Wrinkle in Time」は、遠い宇宙にワープして冒険する物語です。地球人の主人公メグの元に宇宙人フーがやってきて宇宙の旅に誘いますが、そのワープ方法として下記ような説明がされます。
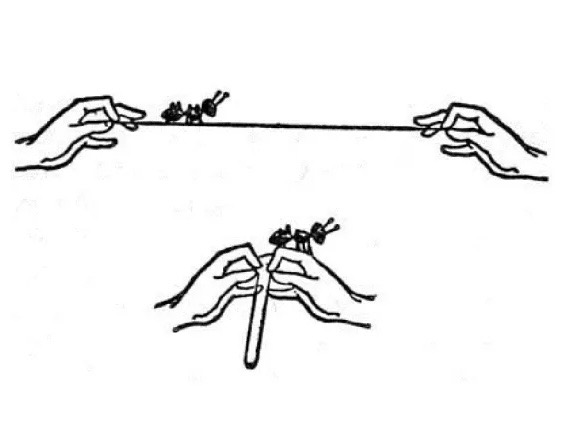
” Mrs Whatsit said, “if a very small insect were to move from the section of skirt in Mrs Who’s right hand to that in her left, it would be quite a long walk for him if he had to walk straight across.”
Swiftly Mrs Who brought her hands, still holding the skirt, together.
“Now, you see,” Mrs Whatsit said, “he would be there, without that long trip. That is how we travel.”引用元：Madeleine L’Engle “A Wrinkle in Time”(1962)
（要点ざっくり翻訳）
「虫がスカートを伝って右手から左手に移動するとしたら、まっすぐに渡るにはかなり長い道のりになるでしょう。」
ミセス・フーはスカートを握ったまま素早く両手を合わせました。
「ほら、長い旅をしなくても虫はそっちにいる。これが私たちの旅の仕方です。」
（邦訳版）
「わたしのスカートの端から端を虫が歩いていくとするとこんなに遠くて時間がかかるわね．けどこうしてスカートの端と端をくっつけてしまえば，ほらすぐに着くでしょう」
このように宇宙移動を説明します。紙ではなくスカートを使っていますが内容としては同じです。特徴的なのはこの小説には挿絵（↑）による説明図示がある事です。
またこの作品は邦題「五次元世界のぼうけん」として1965年に日本出版されています。21エモンの1968以前に邦訳が存在すると言う点でF先生が触れられる可能性はあります。（日本版を読んでないのでこの挿絵部分がどうなっているかは未確認です。少なくとも文章としてはしっかり翻訳されているようですが、挿絵は大幅に改変されているっぽいので挿絵があるのか…）
なお、これの映画版(2018年)では登場シーンは違いますが、主人公の父である博士が宇宙移動のプレゼンをするシーンでスライド映像として空間を折り曲げて2点をくっつけるシーンが出てきます。
狂った世界 SF世界の科学名作11(1965 日本)巻末の解説に写真入りで。
日本語解説として初期に登場した事例がありました。
小説自体はロシアのSF作家アレクサンドル・ベリャーエフのもので、それの邦訳版の巻末解説に編集長福島正実氏による写真と文字で紙曲げワープ説明が登場します。
1965年刊行、日本語で存在、図の写真まであるというのでF先生が知る機会になったとしてもおかしくない事例と言えそうです。日本の最古の紹介例かはわかりませんがもう少し調査を進めたいと思います3。
まとめ。
という事で整理すると、こんな流れの可能性が考えられます。
| 年代 | 事象 | ポイント |
|---|---|---|
| 1880 | 論文で抽象的に「空間を曲げる」という説明が登場 | |
| 1895 | HGウェルズが「紙を曲げて２点移動する」を小説で説明 | 紙曲げ説明の発明 |
| 1953 | 「Starman Jones」で宇宙間移動の説明で「布を折り曲げる」が登場 | 宇宙間移動の説明に使用 |
| 1965 | 狂った世界 SF世界の科学名作11で日本語と図写真で紙曲げ解説が存在。 | 日本語での図入り解説 |
| 1965 | 少なくとも「A Wrinkle in Time」邦訳などで日本にも紙曲げ的説明の文献は存在 | 日本への小説到来例 |
| 1968 | 藤子・F・不二雄が21エモンで漫画のコマに紙曲げ説明を描く | 日本作品での初登場 |
| 1980 | 「ドラえもんのび太の宇宙開拓史」に紙曲げ説明を描く | 日本での知名度向上 |
| (別ライン） | 海外では1990年代くらいから使用例が多くなる | 海外は独自に展開 |
これを調べる前は「もしかしたらF先生が始祖？」「F先生の漫画がハリウッド映画の元ネタになってる？」なんて思っていたのですが、どうやらそうではなく、むしろH.G.ウェルズ等の始祖が芯に存在し、それが日本、海外にそれぞれ枝分かれして育った。という感じなのかなと推測しています。
もしくは、これだけ様々で使われているので小説などでは無く論文やSF解説書などに登場したのかもしれません。引き続き調査は続けたいと思います。
※新情報あれば追記していきますので情報お持ちの方はぜひ教えて下さい。
おまけ：ドラマ「ストレンジャー・シングス 未知の世界」(2016 アメリカ) ワープではなく平行世界の説明として。
2016年7月 Netflix配信ドラマ「ストレンジャー・シングス 未知の世界」の「ノミと曲芸師」の回で、「裏側の世界」という異世界に行く方法として主人公の少年達が博士に質問するシーンで下記の説明が登場します。
クラーク博士「綱渡りの曲芸師がいるとする 綱が我々の世界だ この世界の法則では前か後ろに進むことができる だが曲芸師の隣にノミがいたとしたら？ ノミも前後に進めるよね？」
ドラマ「ストレンジャー・シングス 未知の世界」第5章「ノミと曲芸師」
少年達「はい」
クラーク博士「本題はここからだ ノミは綱の横側も渡る事ができる それどころか… 下だって」
少年達「裏側だ」
博士は紙皿に線を描き、線を綱に見立てて綱の上の世界（現実）と下の世界（並行世界）に分け、人間は綱の下を歩く事はできない（平行世界に行く事はできない）と前提を置いて、異世界に行くためには紙皿を線の所で折り曲げて、重なった所にペンを突き刺し穴を開けゲートを作りそこを通れば平行世界にも行ける（どちらも綱の上になるので人間も歩ける）という説明をします。
いわゆるワープ（長距離移動の短縮方法）ではなく、異世界への移動手段として説明をしているので他のものとは少し違いますが、紙を折り曲げる説明がこのような状況説明にも使える汎用性を伺えるエピソードなので紹介しました。
コメント