ひみつ道具が何でも入っているドラえもんの四次元ポケット。収納量に限界があるような様子は特にありませんが、あの空間は無限なのでしょうか？四次元という言葉自体は無限か有限かとは関係ないのでどちらの可能性もあります。
作中の描写を読み解くと「四次元ポケットの空間は有限だけど、道具は無限に収納できる」なのではないかと思います。理由について説明していきたいと思います。
ポケットの4次元目は、たぶん他の3次元と同じで「方向」
まずは四次元ポケットの「4次元目」が何なのか。SF等では時間を当てはめる事が多いですが必ずしもその必要はなく、数学でよく使われる4次元目は、他の3次元(縦X、横Y、高さZ)と同じくメートル等の距離で表現できるようなもの=「4つめの方向W」と考えます。四次元ポケットは空間の拡張を図ったものなので通常の3次元X,Y,Z軸に加えて4次元目方向W軸を加えたものとして話を進めたいと思います。(空間に時間を加えたものは、ドラえもん世界ではタイムマシン移動中などに見られる「時空間」がありますのででそれとは別と考えた方がいいというのもあります。）
ポケットには「すみ」があるらしい。＝ 空間は有限？
まず四次元ポケットの空間が有限だと考える理由、それは「すみがある」と言うセリフがあるからです。てんコミ41巻「みえないボディガード」で、かげながらという道具を出そうとした際にドラえもんがポケットの中を探りながら「あった！四次元倉庫のすみに。」と言います。
この台詞から、ポケット内の四次元倉庫にはすみが存在する事が明らかになります。すみがあるという事は空間的には有限であるという事です。
ただこの「四次元倉庫」というのがこの話にしか出てこない単語で、「四次元ポケットの空間全体」を意味するのか「四次元ポケットの空間内に存在する収納エリアのようなもの」なのかは不明なので、前者だと考えれば四次元ポケットは有限空間となりますが、後者ならば四次元倉庫が有限なだけでポケットの空間は無限かもしれないとも言えます。（四次元倉庫の考え方は別記事で詳細書いてます）
ポケットの空間が無限なら収納も無限にできる、という事になりますが、名前に同じく「四次元」が入る概念に、すみがあると言われているので、ポケットの空間は有限であるとして話を進めたいと思います。
空間は有限だとしても、無限に収納はできる！（いくらでも入る）
さて、基本的には四次元ポケットには「なんでも入る」「いくらでも入る」と描かれているのでこの条件を満たすような状況を考える必要があります。空間が有限だと収納限界が来るのでは？いえいえ、空間が有限でも道具を無限に入れる事は可能です。
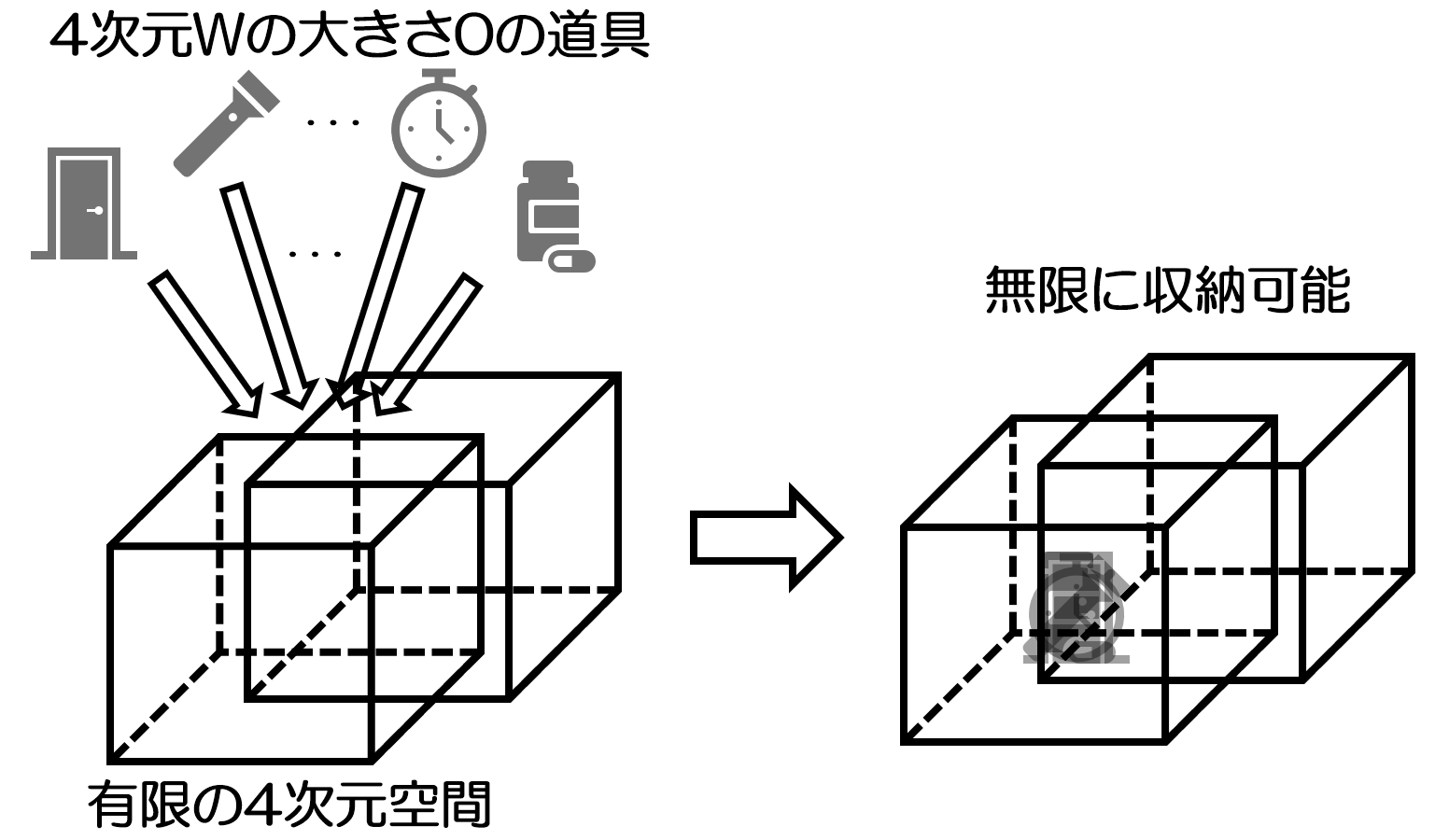
ポイントは、「収納するものの4次元目の大きさ（厚み）が0である」という点に着目する事です。例として四次元ポケットの中がXYZW軸の全て100メートルの空間とした場合は有限空間なわけですが、ひみつ道具は3次元物体なので4次元目であるW軸の大きさは0と言えます。(例えばタケコプターはXYZそれぞれ10cmくらい、Wが0cmという感じ。この世の全ての3次元物体はW0です)この場合、W軸側にいくら積んでも増える事がないため、いくらでも物が入れられる事になります。次元を１つ落として説明するなら、3次元の書類入れに厚みが0の書類をいくら積んでも収納限界を超える事は無い。という感じです。
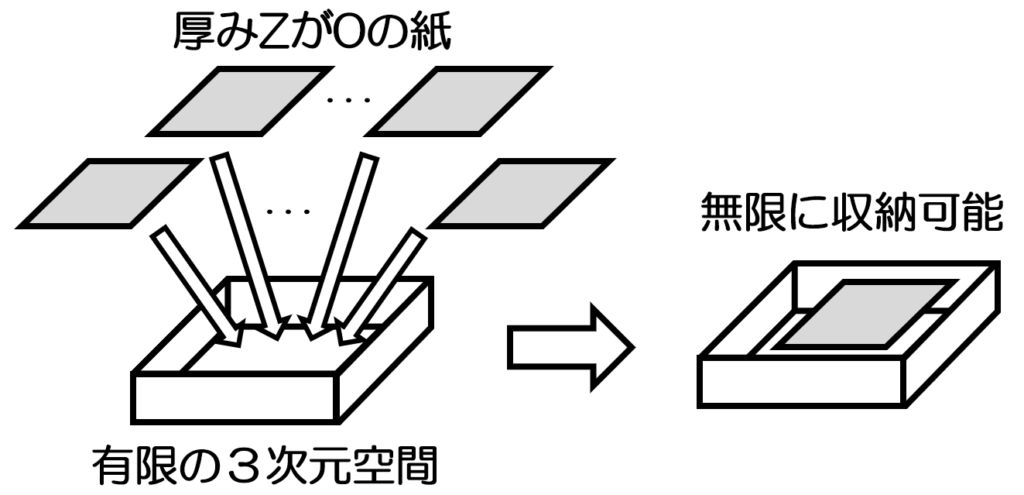
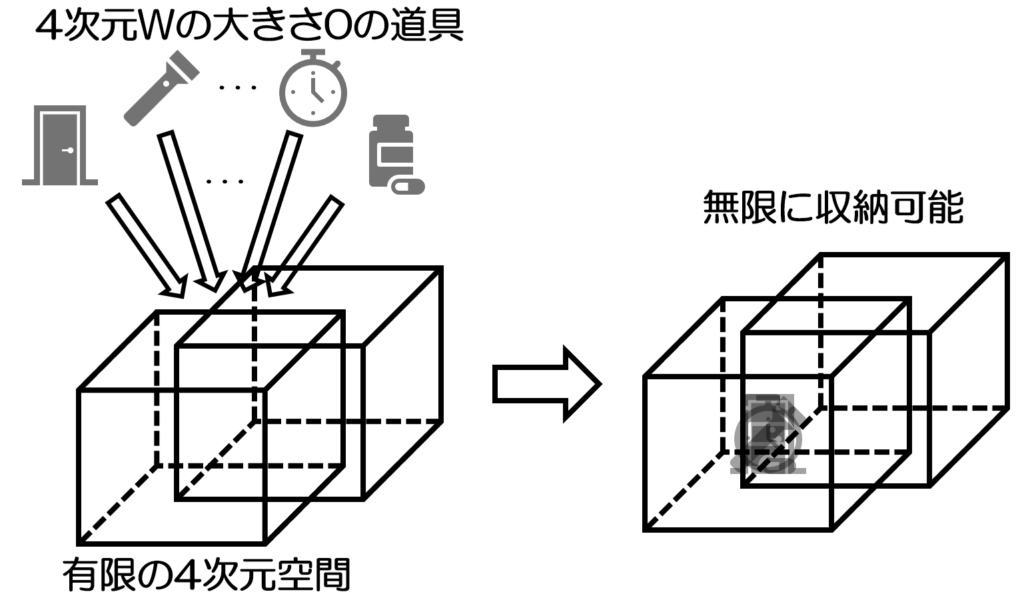
これによって、すみのある有限の4次元空間であっても、入れる物のW軸の大きさが０ならば、いくらでも入るという説明ができます。「いくらでも入る」はこれで説明できます。
「いくらでも入る」＝「なんでも入る」 ではない。
しかし上記の説明ではまだ完全とは言えない所があります。それは「いくらでも入る(数が無制限)＝なんでも入る(大きさが無制限)」ではないという事です。前述の書類入れの説明で言えば、A4サイズの書類入れに厚み0のA4以下の書類を入れる分には無限に入れる事ができるのですが、A4サイズを超える書類は例えば厚み0であろうと1枚も入らないという事になります。
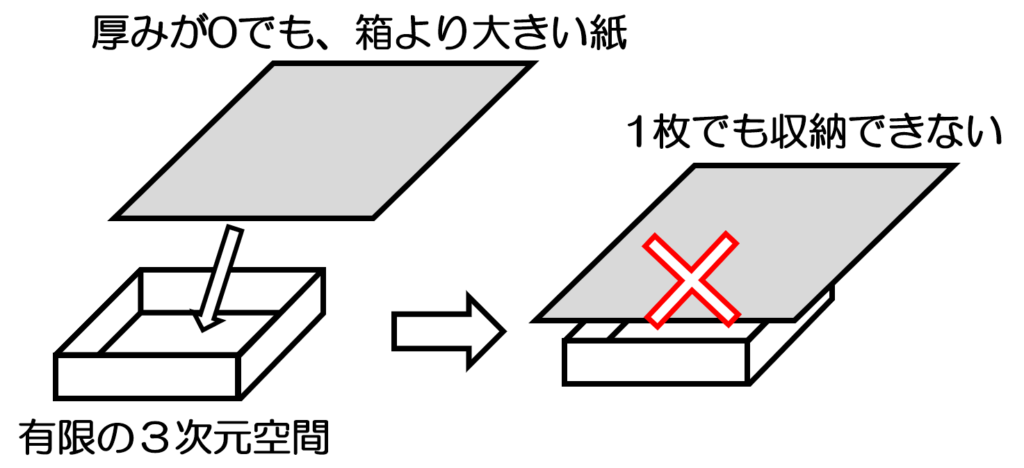
なので先程の説明では空間以上に巨大なひみつ道具があったならばそもそも入らないという事になってしまいます。タケコプターみたいな小型のなら無限個入れられる（いくらでも入る）が、巨大なものは1つも入らない（なんでも入らない）可能性があります。なので、ポケットの空間は有限でもいいけど、大きなものが入れられる程度に広い空間は必要という事になります。
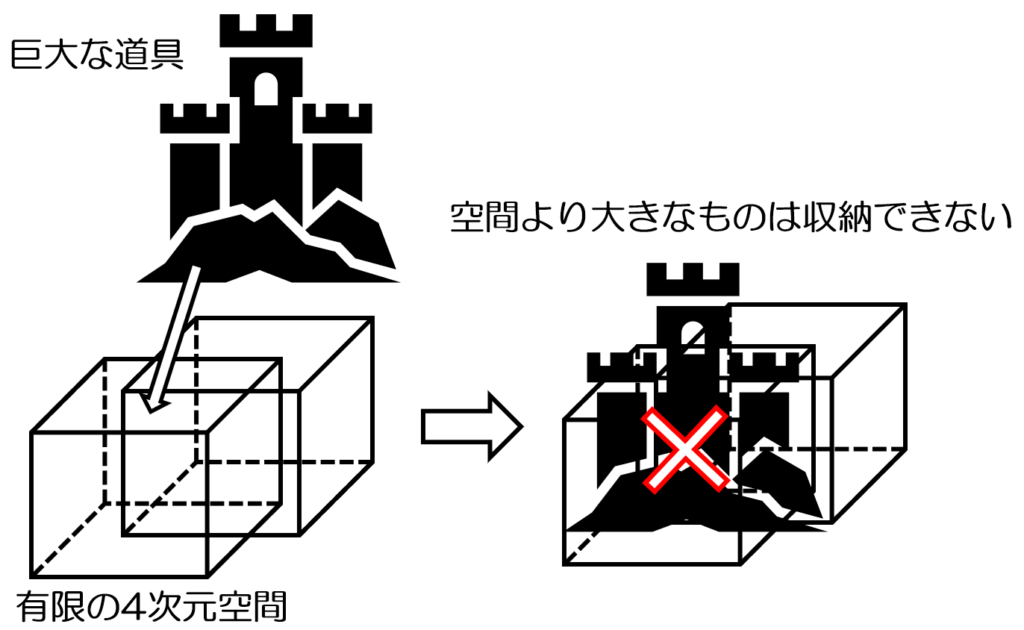
ひみつ道具で最大サイズといえば「風雲ドラえもん城」という日本の城サイズの道具ですが、姫路城などを参考にするならばXYZどれも30メートル近いので、XYZの3次元全てが最低それ以上は必要と言う事になります。まあそれくらいの空間があると考えれば解決となります。（厳密にはそれ以上のサイズは入らないので「なんでも入る」ではなくなりますが、実質的に全ての道具が入るという事です。）
入り口の狭さの問題はこう考えれば大丈夫！かも。「4次元方向に丸める」
有限空間であっても「いくらでも入る」「なんでも入る」はなんとか解決しました。もう１つ問題が残ります。ポケットの入り口です。たとえ中の空間が十分な広さを持っていたとしても、入り口はポケットサイズなので、ここから入れられない限り意味がないのです。
どこでもドアなどポケットより大きい道具が飛び出す様は当たり前に見る光景ですので、何とか説明できるようにしないといけません。
ポケットの入り口が狭いというのは、1次元下げて例えるなら「十分に広いポストなのに投函口が狭い」みたいな感じです。その投函口より大きな紙(厚み0)を入れるにはどうしたよいかという事になります。
解決策はこう考えて見てはどうでしょうか。入れる紙を丸めます。（折り曲げると言ってもいいです）厚みが0なので折り曲げても厚みが増える事はなく、いずれ入り口を通るサイズにまで幅が狭まります。その状態で入り口につっこみ、そして中でまた広がればどんなに大きな紙であっても入り口を通る事ができます。
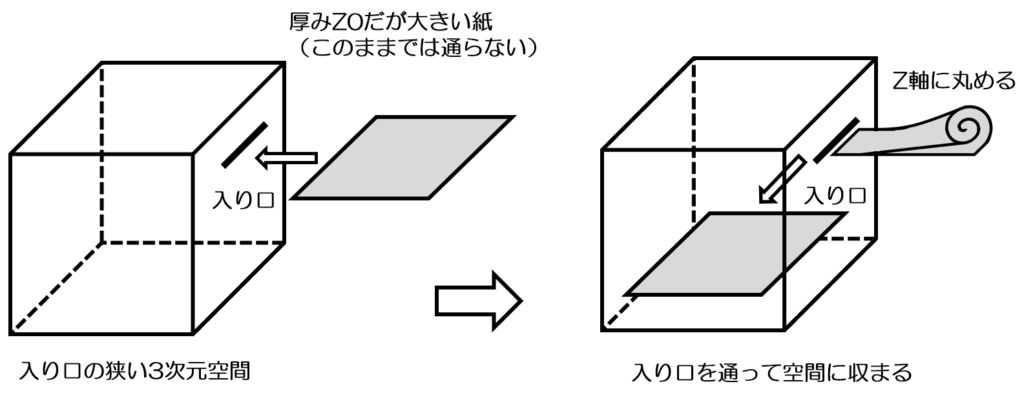
これを応用して4次元で考えると、3次元物体のひみつ道具を、4次元方向を使って「折り曲げる、丸める」をします（全くビジュアルのイメージがわきませんが）。そしてポケットの穴以下のサイズになった時に突っ込んで出し入れするのです。
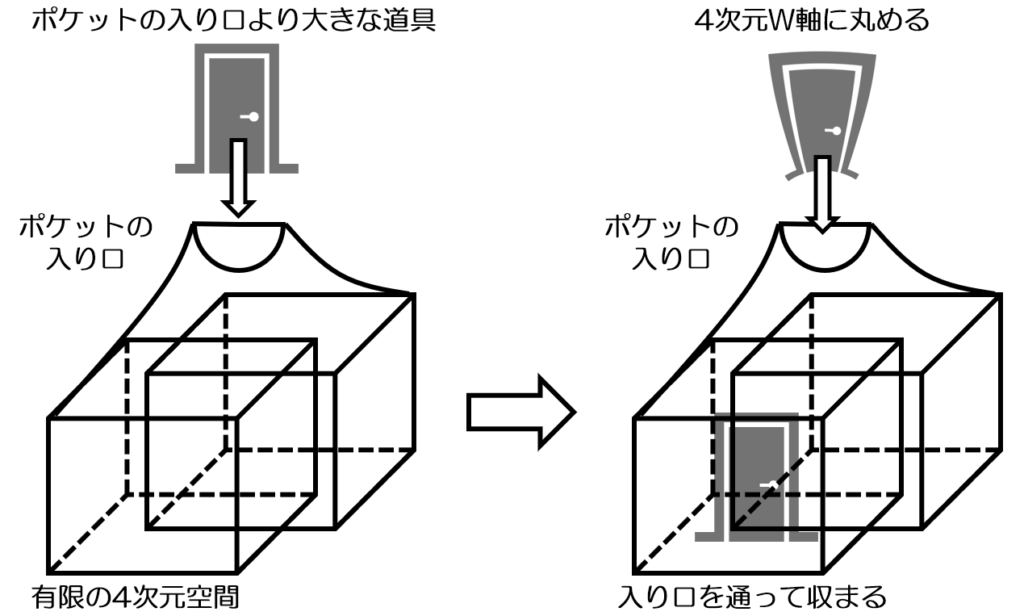
どこでもドアが出てくる時にポケットから歪んで登場するのは、もしかしたらそういう現象を見ていると考えたらつじつまが合うのかも。(数学の専門ではないのでこんな事がができるかわかりません。もし詳しい方いればツッコミください）
終わりに
まあ原作の描写通り、未来の超技術で「何でも入る。いくらでも入る」と考えればいいので小難しい事考えなくてもいいわけですが、一応作中描写の「すみ」という言葉と矛盾なく説明するならどう考えられるかやってみました。
今回は有限なので１個が巨大な物に対しては限界があるとしましたが、それでも空間サイズを極端に広くすれば特に問題ないので、今後もし星をまるごと入れるようなシーンが出てきてしても「有限空間だとしても、めっちゃ広かったんだな」と考えれば特に問題はありません。今後アニメなどでドラえもんが今以上に大きなものポケットに入れるシーンが見れる事を楽しみにしています。
コメント